
-
soit produisant un courant électrique dont la fréquence est déterminée par la vitesse de rotation de la machine : fonctionnement générateur ;
-
soit absorbant un courant électrique dont la fréquence détermine la vitesse de rotation de la machine : fonctionnement moteur.
Au-delà de quelques kilowatts, les machines synchrones sont généralement des machines triphasées. Les alternateurs sont des machines synchrones fonctionnant en génératrice.
Le rotor, souvent appelé roue polaire, est alimenté par une source continue.
Principes généraux [modifier]
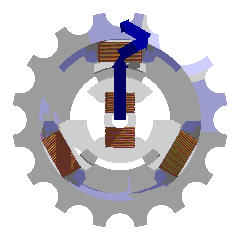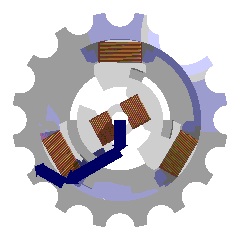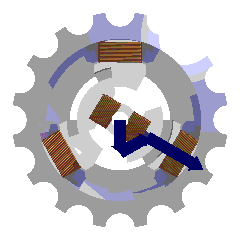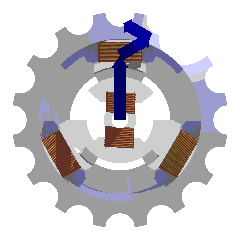
Les courants du rotor créent un champ magnétique tournant dans le stator. Sa fréquence de rotation (sa vitesse) est proportionnelle à la fréquence de l'alimentation électrique. La vitesse de ce champ tournant est appelée vitesse de synchronisme.
L'enroulement au rotor est alimenté par un courant continu ce qui le rend semblable à un aimant. Il peut d'ailleurs être constitué d'aimants permanents, le rotor n'a alors plus besoin d'alimentation. Le champ magnétique du rotor créé cherche en permanence à s'aligner sur celui du stator. C'est le principe de la boussole (qui voit elle par contre un champ magnétique fixe). Cette machine est dite synchrone : le champ du rotor ne peut que tourner à la même vitesse que le champ du stator.
Machine synchrone triphasée [modifier]
Mise en équation [modifier]
Méthode utilisée [modifier]
-
Toutes les grandeurs statoriques sont repérées soit par l'indice S soit par des indices en majuscules.
-
Toutes les grandeurs rotoriques sont repérées soit par l'indice r soit par des indices en minuscules.
L'angle 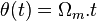 correspond au décalage angulaire entre le stator et le rotor.
correspond au décalage angulaire entre le stator et le rotor.
-
 : Inductances propres d'un enroulement du stator ; d'un enroulement du rotor.
: Inductances propres d'un enroulement du stator ; d'un enroulement du rotor.
-
 : Inductance mutuelle entre deux enroulements du stator.
: Inductance mutuelle entre deux enroulements du stator.
-
 : Valeur maximale de l'inductance mutuelle entre l'enroulement du rotor et un du stator (correspondant à une position pour laquelle θ = 0 ± 2π/3 ).
: Valeur maximale de l'inductance mutuelle entre l'enroulement du rotor et un du stator (correspondant à une position pour laquelle θ = 0 ± 2π/3 ).
La mise en équation n'est opérable que pour une machine à pôles lisses et dont le circuit magnétique est non saturé. Pour les autres machines, on apportera des correctifs permettant (avec plus ou moins d'exactitude) la prise en compte de leurs complexités. Pour la suite on considère une machine pour laquelle :
-
Son circuit magnétique est homogène (entrefer constant) et non saturé. De ce fait, les diverses inductances sont constantes (entrefer constant).
-
Les courants des trois phases statoriques ont la même valeur efficace IS (la machine est assimilable à un récepteur triphasé parfaitement équilibré.
-
Elle possède une seule paire de pôles (machine bipolaire). Les machines multipolaires se ramènent à une machine bipolaire au prix d'une transformation angulaire. A détailler ?
On fixe l'origine des temps de manière à pouvoir écrire :

On en déduit les courants des deux autres phases du stator :


Avec :  , et
, et  : pulsation des courants statoriques
: pulsation des courants statoriques
Au rotor, il n'y a que Ir le courant continu alimentant la bobine du rotor par l'intermédiaire d'un contact glissant sur une bague collectrice.
Remarque
- Si le rotor est constitué d'un aimant, on considèrera une bobine produisant un moment magnétique équivalent, c’est-à-dire traversée par un courant Ir que l'on determine à l'aide de la méthode d'Hopkinson (application du théorème d'Ampère à un circuit magnétique).
- C’est-à-dire :
 la longueur de l'aimant
la longueur de l'aimant respectivement la section moyenne de l'aimant et celle de la bobine
respectivement la section moyenne de l'aimant et celle de la bobine
- On pose :
-


- En supposant que la bobine et l'aimant ont la même section, on obtient :
-

Flux à travers un enroulement statorique [modifier]

Comme :
 , alors
, alors  ,
,

On pose
-
 : inductance cyclique
: inductance cyclique
L'expression du flux devient alors

l'expression du nombre complexe représentant le flux est

avec  la représentation complexe d'un courant sinusoïdal fictif de valeur maximale
la représentation complexe d'un courant sinusoïdal fictif de valeur maximale  et de pulsation
et de pulsation  .
.
En toute rigueur, cette substitution n'est valable qu'en régime établi : aucune modification de la charge ou de l'alimentation. C'est une condition nécessaire pour affirmer que la fréquence de rotation est exactement égale à la fréquence de l'alimentation.
Flux à travers un enroulement rotorique [modifier]
Le flux traversant le rotor est le résultat de deux champ magnétiques
-
Le champ tournant créé par les enroulements statoriques
-
Le champ propre, créé par l'enroulement rotorique qui est constant (courant continu) mais qui tourne mécaniquement à la même vitesse que le précédent (machine synchrone). Avec la même limite qu'au paragraphe précédent : aucune modification de la charge ou de l'alimentation.
Tension aux bornes d'une phase du stator [modifier]


On pose eav la tension à vide, c’est-à-dire la tension lorsque  (tension créée par le seul champ rotorique)
(tension créée par le seul champ rotorique)

Il existe plusieurs modèles équivalents de la machine synchrone suivant le nombre de paramètres dont on veut tenir compte.
Le modèle équivalent de Behn-Eschenburg [modifier]
Le modèle de Ben Eschenburg ne s'applique que si la machine est non saturée et à pôles lisses. C'est le plus simple, il ne tient compte d'aucune saturation ni variation de l'entrefer. Il consiste à remplacer chaque phase de la machine par un ensemble de trois dipôles en série tel que la tension aux bornes de ce dipôle est égale à :

avec :
-
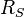 et
et  constants et indépendants du fonctionnement de la machine.
constants et indépendants du fonctionnement de la machine. uniquement proportionnelle à la fréquence de rotation et au courant d'excitation (courant rotorique).
uniquement proportionnelle à la fréquence de rotation et au courant d'excitation (courant rotorique).
Ce modèle convient bien aux gros turboalternateurs de forte puissance. On peut encore simplifier le modèle (et les calculs qui en découlent) en négligeant 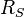 devant
devant  .
.
Le modèle équivalent de Potier [modifier]
Ce modèle est plus complet que celui de Behn-Eschenburg. Il tient compte de la saturation en faisant varier le courant d'excitation en fonction du courant traversant les bobines du stator. Cette modification du courant excitateur fait varier la fcem.
Dans ce modèle on a:


Détermination des paramètres du modèle de Potier [modifier]
Le modèle de Blondel à deux réluctances [modifier]
Il permet de prendre en compte les variations angulaires de réluctance des machines synchrones à pôles saillants.
Articles connexes [modifier]





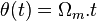 correspond au décalage angulaire entre le stator et le rotor.
correspond au décalage angulaire entre le stator et le rotor. :
:  : Inductance mutuelle entre deux enroulements du stator.
: Inductance mutuelle entre deux enroulements du stator. : Valeur maximale de l'inductance mutuelle entre l'enroulement du rotor et un du stator (correspondant à une position pour laquelle θ = 0 ± 2π/3 ).
: Valeur maximale de l'inductance mutuelle entre l'enroulement du rotor et un du stator (correspondant à une position pour laquelle θ = 0 ± 2π/3 ).



 , et
, et  : pulsation des courants statoriques
: pulsation des courants statoriques la longueur de l'aimant
la longueur de l'aimant respectivement la section moyenne de l'aimant et celle de la bobine
respectivement la section moyenne de l'aimant et celle de la bobine



 , alors
, alors  ,
,
 : inductance cyclique
: inductance cyclique

 la
la  et de pulsation
et de pulsation  .
.

 (tension créée par le seul champ rotorique)
(tension créée par le seul champ rotorique)


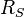 et
et  constants et indépendants du fonctionnement de la machine.
constants et indépendants du fonctionnement de la machine. uniquement proportionnelle à la fréquence de rotation et au courant d'excitation (courant rotorique).
uniquement proportionnelle à la fréquence de rotation et au courant d'excitation (courant rotorique).

